Trong bài viết này, mình sẽ cùng với các bạn tìm hiểu về một thuật toán dùng để sắp xếp các phần tử trong một mảng, thuật toán Merge Sort các bạn nhé!
OK,
Bây giờ, giả sử mình có một mảng gồm các con số có giá trị được sắp xếp như sau:
|
1 |
Integer[] array = { 1, 23, 4, 5, 100, 54 }; |
Thuật toán Merge Sort sẽ chia mảng của mình thành nhiều mảng con, cho đến khi mỗi mảng con chỉ còn một phần tử. Sau đó, nó sẽ so sánh giá trị của các mảng con để gom chúng lại với nhau thành những mảng con đã được sắp xếp. Và kết quả cuối cùng, chúng ta sẽ được một mảng đã được sắp xếp.
Trong ví dụ của mình, khi sử dụng thuật toán Merge Sort thì các bước chạy sẽ xảy ra như sau:
- Bước 1: Chia mảng lớn thành hai mảng con:
|
1 |
1 23 4 _ 5 100 54 |
- Bước 2: Tiếp tục chia nhỏ
|
1 |
1 _ 23 4 _ 5 _ 100 54 |
- Bước 3: Vẫn còn mảng con chứa hơn 2 phần tử nên tiếp tục chia nhỏ
|
1 |
1 _ 23 _ 4 _ 5 _ 100 _ 54 |
- Bước 4: Bởi vì bây giờ tất cả các mảng đã hoàn toàn chứa 1 phần tử, nên giờ chúng ta sẽ so sánh giá trị và gom chúng lại:
|
1 |
1 _ 4 23 _ 5 _ 54 100 |
- Bước 5: Tiếp tục gom:
|
1 |
1 4 23 _ 5 54 100 |
- Kết quả:
|
1 |
1 4 5 23 54 100 |
Như các bạn thấy, sau vài bước chia rồi gom, mảng của mình đã được sắp xếp lại.
Ý tưởng là như thế, vậy giải thuật của thuật Merge Sort là gì? Mình xin nói với các bạn như sau.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
Bắt đầu giải thuật MergeSort MergeSort( biến array là một mảng có n phần tử ) if ( n < 2 ) return array // Bắt đầu chia khai báo biến subArrayFirst là một mảng = array[0] ... array[n/2] khai báo biến subArrayLast là một mảng = array[n/2+1] ... array[n] // Gọi đệ qui để sắp xếp mảng con khai báo biến sortedSubArrayFirst = MergeSort( subArrayFirst ) khai báo biến sortedSubArraySecond = MergeSort( subArrayLast ) // Gom lại return Merge( sortedSubArrayFirst, sortedSubArraySecond ) Kết thúc giải thuật MergeSort |
trong đó giải thuật Merge sẽ như sau:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
Bắt đầu giải thuật Merge Merge( biến subArrayFirst là một mảng, biến subArrayLast là một mảng ) khai báo biến n = số phần tử của mảng subArrayFirst + số phần tử của mảng subArrayLast; khai báo biến sortedArray với số phần tử là n khai báo biến i = 0 khai báo biến j = 0 for (khai báo biến k = 0; k < n; k++) { nếu j < số phần tử của mảng subArrayLast hoặc (i nhỏ hơn số phần tử của mảng subArrayFirst và phần tử tại vị trí i trong mảng subArrayFirst nhỏ hớn phần tử tại vị trí j trong mảng subArrayLast) sortedArray[k] = subArrayFirst[i] tăng giá trị biến i lên 1 ngược lại sortedArray[k] = subArrayLast[j] tăng giá trị biến j lên 1 } Kết thúc giải thuật Merge |
OK, sau đây mình sẽ trình bày các bạn cách hiện thực thuật toán Merge Sort với ngôn ngữ Java như sau:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
package com.huongdanjava.mergesort; import java.lang.reflect.Array; import java.util.Arrays; import java.util.Comparator; public class MergeSort { public <K> K[] doMergeSort(K[] arrayNeedToSort, Comparator<K> comparator) { int n = arrayNeedToSort.length; if (n < 2) { return arrayNeedToSort; } int middle = n / 2; K[] subArrayFirst = Arrays.copyOfRange(arrayNeedToSort, 0, middle); K[] sortedSubArrayFirst = doMergeSort(subArrayFirst, comparator); K[] subArrayLast = Arrays.copyOfRange(arrayNeedToSort, middle, n); K[] sortedSubArraySecond = doMergeSort(subArrayLast, comparator); return merge(sortedSubArrayFirst, sortedSubArraySecond, comparator); } private <K> K[] merge(K[] sortedSubArrayFirst, K[] sortedSubArraySecond, Comparator<K> comparator) { int n = sortedSubArrayFirst.length + sortedSubArraySecond.length; K[] sortedArray = (K[]) Array.newInstance(sortedSubArrayFirst[0].getClass(), n); int i = 0; int j = 0; for (int k = 0; k < n; k++) { if (j == sortedSubArraySecond.length || (i < sortedSubArrayFirst.length && comparator.compare(sortedSubArrayFirst[i], sortedSubArraySecond[j]) < 1)) { sortedArray[k] = sortedSubArrayFirst[i++]; } else { sortedArray[k] = sortedSubArraySecond[j++]; } } return sortedArray; } } |
Trong hiện thực thuật toán Merge Sort này, mình đã sử dụng thêm interface Comparator để làm so sánh giữa hai đối tượng của cùng một class.
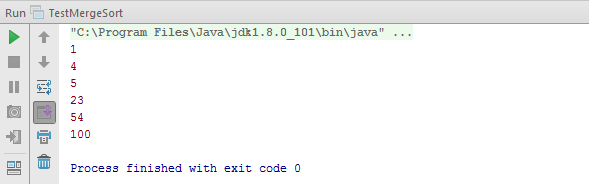
Sau đây, mình sẽ sử dụng code ở trên để làm một ví dụ xem sao:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
package com.huongdanjava.mergesort; import java.util.Comparator; public class TestMergeSort { public static void main(String args[]) { MergeSort mergeSort = new MergeSort(); Integer[] array = {1, 23, 4, 5, 100, 54}; Comparator<Integer> comparator = new Comparator<Integer>() { public int compare(Integer o1, Integer o2) { if (o1 > o2) return 1; else if (o1 == o2) return 0; else return -1; } }; Integer[] sortedArray = mergeSort.doMergeSort(array, comparator); for (Integer o : sortedArray) { System.err.println(o.intValue()); } } } |
Kết quả: